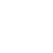Elastic waves in complex media
Elastic waves in complex media
Elastic waves in complex media
About
 We are interested in mechanical structures introducing strong dispersion effects or spectacular nonlinear phenomena. We are interested in granular media, soft nonlinear solids, instable structures, flexible metamaterials and topological crystals, among others.
We are interested in mechanical structures introducing strong dispersion effects or spectacular nonlinear phenomena. We are interested in granular media, soft nonlinear solids, instable structures, flexible metamaterials and topological crystals, among others.
Our goal is to develop model systems enabling the observation of extreme wave effects. Our research has applications in the fields of soft-robotics, vibrations mitigation, or energy harvesting solutions. We are also interested in developing platforms providing analogies with biomechanical processes, to gain understanding about the behavior of the human body.
Interested in joining us? Check the Job Offers.
Contact
Elastic waves in complex media
Laboratoire d’Acoustique de l’Université du Mans (LAUM)
Av. Olivier Messiaen, 72085 Le Mans, France
Maxime.Lanoyuniv-lemans.fr
Research
Extreme wave phenomena in flexible elastic metamaterials
 A flexible elastic meta-lattice allowing the observation of solitary waves
A flexible elastic meta-lattice allowing the observation of solitary waves
Flexible elastic metamaterials (flexEMs) are defined as engineered structures that can deform substantially, repeatedly and reversibly. Although recent advances have improved our understanding of the quasi-static mechanical properties of flexEMs, there are not many studies on their nonlinear dynamic response. We are working with two types of flexEMs. One consisting of (i) rotating rigid units (particles of different shapes) coupled with soft elastic elements and (ii) a lattice of coupled buckled beams, a bistable mechanical metamaterial. Using various analytical and numerical techniques, we were able to find several nonlinear wave solutions, including solitons, breathers and wave extreme events, that can be supported by these types of flexEMs.
Related publications:
- https://www.sciencedirect.com/science/article/pii/S2352431624000798
- https://journals.aps.org/pre/abstract/10.1103/PhysRevE.107.054212
Dynamical mechanical instabilities
Slender structures can undergo different forms of mechanical instabilities, leading to potentially large and rapid deformation of the object. For a long time, they have been regarded as detrimental-one would rather not use a bridge that buckles!-, but over the last 20 years this opinion have shifted. Mechanical instabilities can be indeed be used to pattern a surface, achieve large or rapid motion, as illustrated in different natural processes, from the shape of living tissues to the fast motion of carnivorous plants. Now, these nonlinear phenomena are more and more used in manufactured objects, at low scales in MEMS, or in flexible metamaterials to achieve exotic properties. It is therefore important to understand instabilities and find ways to control their characteristics. To do so we investigate how dynamics affect the instabilities. We have shown how rapid actuation allows to lower the instability threshold and generates complex dynamics in the structure. More generally, we are interested in dynamically triggered instabilities as well as dynamics of the instability itself.
 Chronophotography of a snap-through instability in a beam
Chronophotography of a snap-through instability in a beam
Space & time-dependent soft structures
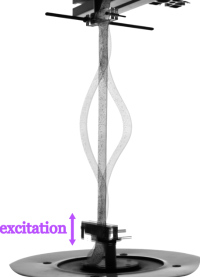 Parametric instability in a soft stripAnother spectacular mechanical instability occurs when a string undergoes a temporal modulation of its tension. As evidenced in the XIXth century by Franz Melde, such a string exhibits large transverse deformations together with a marked sub-harmonic response. We have recently evidenced an atypical response emerging in the case of a very soft string. These results highlight the rich physics of systems for which the modulation becomes spatio-temporal. Our group investigates the nonlinear dynamics of soft structures (string, strips, plates and lattices).
Parametric instability in a soft stripAnother spectacular mechanical instability occurs when a string undergoes a temporal modulation of its tension. As evidenced in the XIXth century by Franz Melde, such a string exhibits large transverse deformations together with a marked sub-harmonic response. We have recently evidenced an atypical response emerging in the case of a very soft string. These results highlight the rich physics of systems for which the modulation becomes spatio-temporal. Our group investigates the nonlinear dynamics of soft structures (string, strips, plates and lattices).
Topology & nonlinearity
We investigate structures for advanced control of elastic waves using concepts and tools from topological materials and nonlinear dynamics. The recent discovery of topological materials in condensed matter physics has led to the emergence of a new notion of topology associated with the intrinsic wave dispersion of a structure. As a result, numerous mechanical designs have been developed that exhibit non-trivial and robust energy localization. However, the great majority of these works is limited in the linear regime. Using analytical, continuation and bifurcation techniques, we have studied the interplay of nonlinearity and topology, revealing new nonlinear topological solutions and self-induced topological transitions. In addition, recently we have introduced a new family of finite-frequency mechanical metamaterials. Here, robust topological properties appear in deformation coordinates, while topological edge waves appear for free boundaries.
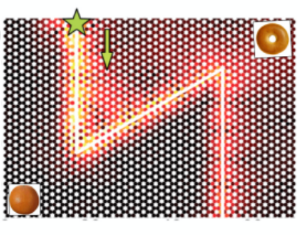 Robust wave guiding process powered by topological insulationRelated publications:
Robust wave guiding process powered by topological insulationRelated publications:
Publications
Recent publications (since 2022)
2024
- A. Delory, D. A. Kiefer, M. Lanoy, A. Eddi, C. Prada, and F. Lemoult, “Viscoelastic dynamics of a soft strip subject to a large deformation,” Soft Matter, vol. 20, no. 9, pp. 1983–1995, 2024.
-
A. Delory, C. Prada, M. Lanoy, A. Eddi, M. Fink, and F. Lemoult, “Elastic wavepackets crossing a space-time interface,” arXiv preprint, arXiv:2406.15100, 2024.
-
T. Lee, B. M. Manda, X. Li, G. Theocharis, and C. Daraio, “Control of multimodal topological edge modes in magnetoelastic lattices,” Phys. Rev. Applied, vol. 21, no. 2, 024049, 2024.
-
K. Prabith, G. Theocharis, and R. Chaunsali, “Nonlinear corner states in a topologically nontrivial kagome lattice,” Physical Review B, vol. 110, no. 10, 104307, 2024.
-
A. Paliovaios, V. Achilleos, G. Theocharis, D. Frantzeskakis, and N. Stefanou, “Time-periodic Klein-Gordon media: Tunable wave-vector gaps and Dirac dispersion with an exceptional point of degeneracy,” Physical Review A, vol. 109, no. 6, 062229, 2024.
-
A. Paliovaios, G. Theocharis, V. Achilleos, and V. Tournat, “Transition waves in bistable systems generated by collision of moving breathers,” Extreme Mechanics Letters, vol. 71, 102199, 2024.
2023
-
H. Bense, E. Siéfert, and F. Brau, “Measurement of capillary forces using two fibers dynamically withdrawn from a liquid: Evidence for an enhanced Cheerios effect,” Phys. Rev. Lett., vol. 131, 184003, 2023.
-
R. Chaunsali, P. G. Kevrekidis, D. Frantzeskakis, and G. Theocharis, “Dirac solitons and topological edge states in the -Fermi-Pasta-Ulam-Tsingou dimer lattice,” Phys. Rev. E, vol. 108, no. 5, 054224, 2023.
-
X. Shi, R. Chaunsali, G. Theocharis, H. Huang, R. Zhu, and J. Yang, “Topological phase transition in a disordered elastic quantum spin Hall system,” Physical Review B, vol. 108, no. 5, 054205, 2023.
-
F. Allein, A. Anastasiadis, R. Chaunsali, I. Frankel, N. Boechler, F. K. Diakonos, and G. Theocharis, “Strain topological metamaterials and revealing hidden topology in higher-order coordinates,” Nature Communications, vol. 14, no. 1, 6633, 2023.
-
A. Demiquel, V. Achilleos, G. Theocharis, and V. Tournat, “Modulation instability in nonlinear flexible mechanical metamaterials,” Phys. Rev. E, vol. 107, no. 5, 054212, 2023.
2022
-
A. Delory, F. Lemoult, M. Lanoy, A. Eddi, and C. Prada, “Soft elastomers: A playground for guided waves,” The Journal of the Acoustical Society of America, vol. 151, no. 5, pp. 3343–3358, 2022.
-
J. Liu, M. Teunisse, G. Korovin, I. R. Vermaire, L. Jin, H. Bense, and M. van Hecke, “Controlled pathways and sequential information processing in serially coupled mechanical hysterons,” Proceedings of the National Academy of Sciences, vol. 121, no. 22, e2308414121, 2022.
-
A. Ngapasare, G. Theocharis, O. Richoux, C. Skokos, and V. Achilleos, “Wave packet spreading in disordered soft architected structures,” Chaos, vol. 32, 053116, 2022.
-
L.-Y. Zheng, S. Qu, F. Allein, T. Thréard, V. Gusev, V. Tournat, and G. Theocharis, “Direct observation of edge modes in zigzag granular chains,” Journal of Sound and Vibration, vol. 526, 116761, 2022.
-
B. M. Manda, R. Chaunsali, G. Theocharis, and C. Skokos, “Nonlinear topological edge states: From dynamic delocalization to thermalization,” Phys. Rev. B, vol. 105, 104308, 2022.
-
Y. Miyazawa, C. Chen, R. Chaunsali, T. S. Gormley, G. Yin, G. Theocharis, and J. Yang, “Topological state transfer in Kresling origami,” Communications Materials, vol. 3, 1-10, 2022.
Group members

|
Hadrien Bense CNRS Scientist Hadrien.Benseuniv-lemans.fr
|
Emmanuel Brasseur Research engineer Emmanuel.Brasseuruniv-lemans.fr |
Matthieu Checkroun Assistant professor Matthieu.Checkroun univ-lemans.fr |
|
Maxime Lanoy Assistant professor Maxime.Lanoyuniv-lemans.fr |
Georgios Theocharis CNRS Scientist Georgios.Theocharis univ-lemans.fr |
Vincent Tournat CNRS Scientist Vincent.Tournat univ-lemans.fr |
|
Bertin Many Manda Postdoctoral fellow bertin.many_mandauniv-lemans.fr |
Marina Terzi Postdoctoral fellow marina.terziuniv-lemans.fr |
Alexis Mousseau PhD student alexis.mousseau.etuuniv-lemans.fr
|
|
Hermann Kwabong PhD student Herman.Kwabong_Njofanguniv-lemans.fr |
Apostolos Paliovaios PhD student Apostolos.Paliovaios.Etuuniv-lemans.fr
|
Eleonore Duval PhD student eleonore.duval.etuuniv-lemans.fr |
|
Athina Galani Master student |
|
|